◾문제
현대자동차그룹 연구소에서는 임직원들의 편의를 위해 출퇴근 통근 버스를 제공하고 있다.
퇴근 시간이 되면 연구소 주차장에는 수 많은 버스들이 일렬로 주차되어 있다. 퇴근 버스는 번호순서 대로 출발해야 하는데, 주차장은 폭이 좁아 앞의 버스가 모두 나가야 뒤의 버스가 나갈 수 있는 구조로 되어 있다.
버스를 순서에 맞게 출발시키기 위해, 연구소 주차장의 맞은편에 임시 주차장을 추가로 건설하였다. 이렇게 만든 임시 주차장은 출입구가 하나밖에 없는 데다가, 폭이 좁아서 스택(Stack)처럼 맨 처음 들어간 버스는 맨 마지막에 나올 수 있다. 또한, 한 번 임시 주차장으로 이동했던 버스는 다시 원래의 주차장으로 이동할 수 없다.
위와 같은 상황에서 퇴근 버스를 번호 순서대로 출발시키는 문제는 스택 정렬로 모델링할 수 있다.
스택 정렬이란, $a_1, a_2, ..., a_n$ 을 정렬할 때, 앞에서부터 순서대로 스택에 Push하거나, 스택에서 Pop하여 출력하는 것을 골라서 반복하여, 정렬된 순서로 출력되도록 하는 것이다. Stack은 가장 나중에 들어간(Push) 자료가 가장 먼저 꺼내지는(Pop) 자료구조이다. 즉, 주어진 수가 3, 1, 2의 세개라면, 3을 Push (스택에 3만 저장됨), 1을 Push (스택에 3, 1이 저장됨), 스택에서 Pop 하여 출력 (스택에 가장 나중에 들어간 1이 Pop 되어 출력됨), 2를 Push, Pop하여 출력 (2가 출력됨), Pop하여 출력으로 마지막으로 3을 출력할 수 있다.
아래의 그림은 이러한 과정을 보여준다.
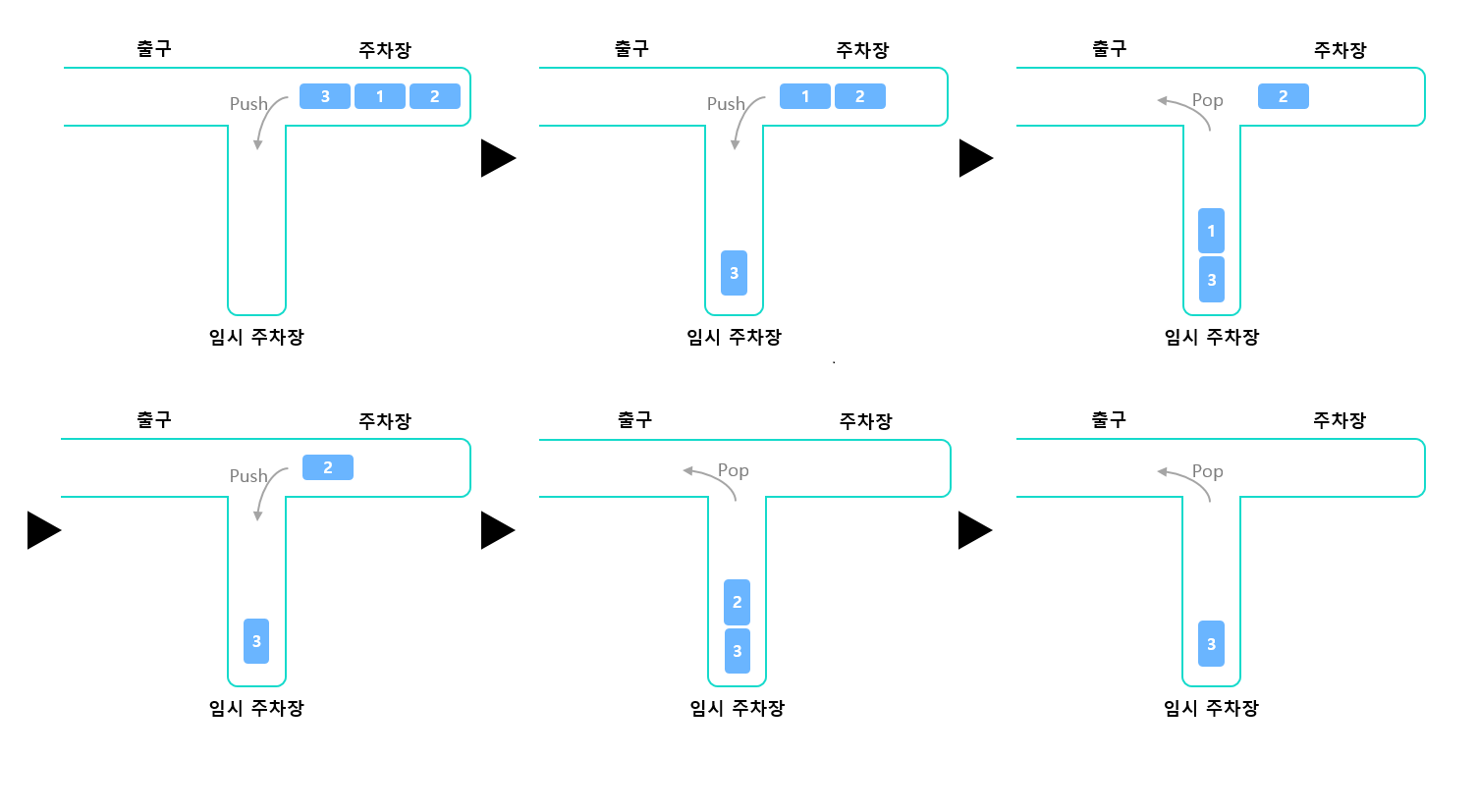
하지만, 모든 경우의 순열을 스택 정렬을 통해 순서대로 정렬할 수 있는 것은 아니다. 주어지는 입력에 따라 스택 정렬이 불가능한 경우도 있다.
임의의 자연수 i < j < k에 대해서, $a_i$ < $a_j$ 이고 $a_i$ > $a_k$ 인 경우가 하나라도 있으면 정렬이 불가능하다는 것이 증명되어 있다. 즉, 버스들의 번호가 $a_1, a_2, …, a_n$ 와 같이 주어질 때, 이와 같은 (i, j, k)의 사례가 있다면, (오름차순) 순서대로 스택 정렬이 불가능하다.
연구소에서 개발자로 일하고 있는 당신은, 연구소 주차장에 주차되어 있는 버스들이 임시 주차장을 활용하여 번호 순서대로(오름차순) 출발할 수 있는지 알아보는 프로그램을 만들어보려고 한다. 버스들이 번호 순서대로 출발하는 것이 불가능한 지 알아보기 위해, 그것을 증명할 수 있는 서로 다른 (i, j, k)의 케이스들을 몇 개나 찾을 수 있는 지 출력하여라. (만약, 출력값이 0이라면 버스들이 위의 과정을 통해, 순서대로 출발할 수 있음을 의미한다.)
◾제약조건
- 3 ≤ N ≤ 5,000인 정수
- 버스 번호는 서로 중복되지 않는다.
◾입력형식
- 첫 번째줄에 수열의 크기 N이 주어진다.
- 두 번째줄에 1부터 N까지의 정수가 재배열된 수열이 공백을 사이에 두고 주어진다.
◾출력형식
- 문제에서 주어진 조건을 만족하는 서로 다른 (i, j, k) 순서쌍의 개수를 출력한다.
입력예제1
3
3 1 2출력예제1
0입력예제2
3
2 3 1출력예제2
1 첫 번째 위치에는 2번 버스, 두 번째 위치에는 3번 버스, 그리고 세 번째 위치에는 1번 버스가 기다리고 있기 때문에($a_1=2, a_2=3, a_3=1$), 순서쌍이 (1,2,3)일 때, 문제의 조건에 따라 순서대로 출발이 불가능함을 증명할 수 있다.
입력예제3
4
4 3 1 2출력예제3
0입력예제4
5
4 2 5 3 1출력예제4
4 순서쌍이 (1, 3, 4), (1, 3, 5), (2, 3, 5), (2, 4, 5)인 경우에 각각의 버스 번호들의 쌍이 [4번, 5번, 3번], [4번, 5번, 1번], [2번, 5번, 1번], [2번, 3번, 1번]이 되어, 버스를 순서대로 출발시킬 수 없음을 증명할 수 있다.
◾풀이 및 고찰
i < j < k 에서, $a_i < a_j, a_i > a_k$를 만족하는 쌍을 찾는 문제이다.
i, j, k를 변수로 삼중 반복문을 사용할 수 있다. 데이터 사이즈는 5,000이다. 따라서, $O(N^3)$의 경우 125,000,000,000이 된다. 당연히 시간 초과이다. 그래서 이중 포인터를 생각했는데, 그래도 N의 power가 바뀌는 것은 아닌 것 같았다.
결국, 해설을 보고 풀었다.
k로 고를 수 있는 경우의 수 미리 계산하기k를 고르기 위해서는,j≤k≤N인 자연수 k들 중 $a_i > a_k$ 를 만족하는 경우를 찾아내야 한다.- 이때, $a_i$ 로 가능한 값들이 1 이상 N 이하의 자연수로 제한되어 있기 때문에, 1 이상 N 이하의 특정한 자연수보다 작도록 $a_k$ 를
j<k≤N에서 미리 계산할 수 있는 방법을 구간합을 통해 구할 수 있다. - 즉, 임의의 자연수
X(1≤X≤N)에 대하여,arr\[X\]\[j\]를 j번째보다 오른쪽에 있는 숫자들 중, X보다 값이 작은 것들의 개수라고 정의할 수 있다. - 각각의 X에 대해, j가 N일 때 N번째보다 오른쪽에 있는 숫자는 없으므로,
arr\[X\]\[N\]= 0이고, j가N-1일 때는 다음과 같이 계산이 가능하다. arr\[X\]\[N-1\] = a\[N-1\] < X ? 1 : 0- 이어서,
arr\[X\]\[j\] = arr\[X\]\[j+1\] + (a\[j\] < X ? 1: 0) - j가 1이 될 때 까지 반복하므로, 총 시간복잡도는 $O(N^2)$ 이다.
- arr를 이용해서 정답 구하기
- i<j와
$a\_i<a\_j$를 동시에 만족하는 모든 i와 j에 대하여arr\[a\[i\]\]\[j\]를 더해주면 모든 순서쌍의 개수를 구할 수 있다. 여기서 주의할 점은, N이 5,000까지이므로 가능한 순서쌍은 $_{5000}{C}_3$개 이므로, int 변수에 값을 더하면 overflow가 발생할 수 있다. 따라서, 64비트 정수형을 사용해주어야 한다.
- i<j와
public static void main(String args[]) throws Exception
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] buses = new int[N]; // 버스 배열
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i = 0; i < N; i++)
buses[i] = Integer.parseInt(st.nextToken());
System.out.println(solution(buses));
}
// 솔루션 함수
public static long solution(int[] buses){
long answer = 0;
int[][] arr = new int[buses.length+1][buses.length+1]; // arr[x][j] : j의 우측에 있는 버스 중 x보다 값이 큰 버스의 수 구간합 변수
// 구간합 연산 O(N^2)
for(int x = 1; x <= buses.length; x++){
// 점화식 초기값
arr[x][buses.length-1] = buses[buses.length-1] < x ? 1 : 0;
// 점화식 수행
for(int j = buses.length-2; j > 0; j--){
arr[x][j] = arr[x][j+1] + (buses[j] < x ? 1 : 0);
}
}
// i < j를 만족하는 (i, j)쌍들 구간합 가산
for(int i = 0; i < buses.length - 2; i++){
for(int j = i+1; j < buses.length - 1; j++){
if(buses[i] > buses[j])
continue;
answer += arr[buses[i]][j];
}
}
return answer;
}'Algorithm > Problems' 카테고리의 다른 글
| [JAVA]수 찾기(Baekjoon) (0) | 2023.02.15 |
|---|---|
| [JAVA]플로이드(Baekjoon) (0) | 2023.02.15 |
| [JAVA]문자열 폭발(Baekjoon) (0) | 2023.02.14 |
| [JAVA]징검다리 건너기(Programmers, 카카오) (0) | 2023.02.14 |
| [JAVA]뒤에 있는 큰 수 찾기(Programmers) (0) | 2023.02.14 |